index
 Sujet
Sujet [
Version PDF]
A un réseau
R=(
X,
U,
c) où circule un flôt
f, on associe un réseau
d'écart
R'=(
X,
U',
c') définit par :
U' contient 2 fois plus d'éléments que
U, à
u=(
x,
y)
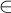 U
U correspond 2 arcs :
u+=(
x,
y)
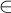 U
U' et
u-=(
y,
x)
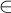 U
U' avec
c'(
u+)=
c(
u)-
f(
u) et
c'(
u-)=
f(
u)
1 Recherche d'un flôt maximum
1.1
Adapter l'algorithme de
Ford-Fulkerson pour obtenir le flôt maximum dans un réseau d'écarts.
Justifier les modifications.
1.2
Programmer cet algorithme et
le tester sur un exemple judicieusement choisi.
Commenter.
Si chaque arc de
U a un coût unitaire
l(
u), le coût de transport de la quantité
f(
u) circulant sur
u est
f(
u)*
l(
u).
Le coût total de transport pour le flôt
f sur le réseau
R est
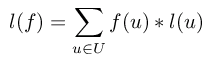
Sur le réseau d'écart
R' :
 u
u
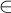 U
U,
l'(
u+)=
l(
u) et
l'(
u-)=-
l(
u).
Pour construire un algorithme donnant le flôt maximum à coût minimum, il existe 2 stratégies qui utilisent
le réseau d'écarts :
Le chemin amplificateur
C de
s à
p est constitué d'arcs de capacités > 0, n'empruntant
pas l'arc de retour.
Sa longueur
l(
C) est égale à la somme des coûts unitaires des arcs qui le composent.
Montrer qu'en combinant l'algorithme modifié de Ford-Fulkerson et un
algorithme de plus court chemin,
il est possible d'obtenir un algorithme donnant le flôt cherché.
2.2 Méthode du circuit réducteur de coût
Un circuit réducteur est constitué d'arcs de capacités > 0, dont la longueur est négative et n'empruntant
pas l'arcs de retour.
Montrer qu'en partant d'un flôt maximum obtenu par l'algorithme de Ford-Fulkerson de coût quelconque,
il est possible en utilisant des circuits réducteurs d'obtenir le résultat.
Programmer au moins un des 2 algorithmes,
le (ou les)
tester sur un exemple intéressant.
Commenter.
 index
index
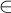 U correspond 2 arcs :
u+=(x, y)
U correspond 2 arcs :
u+=(x, y) 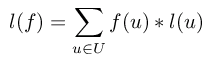
 u
u